Gehirntheorie der Wirbeltiere
ISBN
978-3-00-064888-5
Monografie von Dr. rer. nat. Andreas Heinrich Malczan
4.2 Die zweite Erweiterungsphase des urtümlichen Spinocerebellums
Das Spinocerebellum wird oft als das höchste Integrationssystem der einfacheren Wirbeltiere angesehen. Seine Entwicklung erfolgte zeitweilig sprunghaft, indem neue Signalwege erschlossen wurden.
Wir postulieren in dieser Monografie eine zweite Erweiterungsphase des Spinocerebellums.
Diese zweite Erweiterungsphase begann mit dem Prinzip der Signalredundanz. Signale wurden nicht mehr auf Einzelaxonen übertragen, sondern auf Axonbündeln. So konnte der Ausfall einzelner Neuronen die Signalübertragung nicht wesentlich behindern. Ein Signal wurde zunächst durch Signaldivergenz auf mehrere Axone eines Axonbündels verteilt, lief auf ihnen zur Zielstruktur und wurde dort durch Signalkonvergenz wieder zusammengeführt.
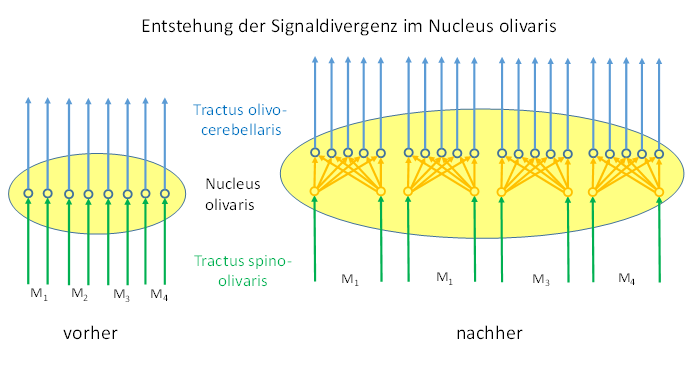
- Abbildung 22 - Die Herausbildung der Signaldivergenz im Nucleus olivaris
Damit erforderte die redundante Signalübertragung sowohl eine Divergenzstruktur als auch eine Konvergenzstruktur. Beim Cerebellum entwickelte sich der Nucleus olivaris zur Divergenzstruktur, während der Nucleus ruber die Konvergenzstruktur bildete. Die Entwicklung des Redundanzprinzips schuf die Grundlage für die spätere Intelligenz der Wirbeltiere.
Die Divergenzstruktur werden wir in dieser Monografie als (neuronales) Divergenzgitter bezeichnen.
Die Signaldivergenz im Nucleus olivaris setzte voraus, dass die Inputaxone nach Signalpaaren geordnet wurden. Dies beruhte auf einer Paarbildung von Muskeln. Jeweils ein Muskel und sein motorischer Gegenspieler bildeten ein Muskelpaar, welches zu einem Gelenk gehörte. Die Signale ihrer Muskelspindeln waren signalverwandt und bildeten ein Paar von zueinander komplementären Signalen, weil das eine Signal durch Inversion aus dem anderen gebildet werden konnte, wozu das Spinocerebellum ja auch da war. Analoges gilt für die Signale der zugehörigen Sehnenorgane, die die Muskelspannung messen konnten.
Die Signaldivergenz fand nur zwischen komplementären Signalen statt. Sie setzte voraus, dass die Anzahl der Rumpfmuskeln stärker anstieg. Befand sich bei einer sehr geringen Rumpfmuskelanzahl der Gegenspieler meist auf der kontralateralen Körperhälfte, so änderte sich dies mit ihrer zahlenmäßigen Zunahme, zumal neben reinen Biegegelenken auch Drehgelenke entstanden. Hier befand sich jeder Muskel in der Nähe seines Gegenspielers, wenigstens am Angriffspunkt der Zugkräfte.
Das Muskelspindelsignal eines Muskels wurde im Nucleus olivaris auf eine ganze Reihe von Outputneuronen verteilt, die gleichzeitig das Muskelspindelsignal des Gegenspielermuskels empfingen.
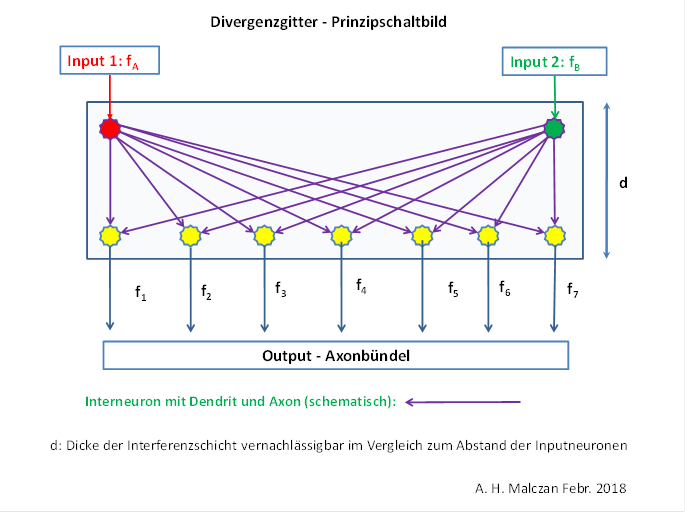
Abbildung 23 - Divergenzgitter im Nucleus olivaris - Prinzipschaltbild
Theorem der Signaldivergenz im Nucleus olivaris
Das Muskelspindelsignal eines Muskels und das seines motorischen Gegenspielers erreichten als komplementäres Signalpaar den Nucleus olivaris über den Nucleus ruber. Gleiches gilt für die Rezeptorsignale der Sehnenorgane. Jedes dieser Signalpaare projizierte auf mehr als zwei Outputneuronen, so dass durch die auftretende Redundanz der Ausfall einzelner Outputneuronen kompensiert werden konnte. Die Anzahl der Outputneuronen pro Input-Signalpaar wuchs im Verlaufe der Evolution stetig an. Jedes der zwei Signale projizierte auf die gleiche Menge von Outputneuronen des Nucleus olivaris, die sich auf der Verbindungsgeraden über den beiden Neuronen anordneten. Dadurch trat eine Signaldivergenz beider Signale auf.
Für die beteiligten zwei Inputneuronen legen wir eine spezielle Bezeichnung fest.
Definition: Erzeugende Inputneuronen des Nucleus olivaris
Die zwei Inputneuronen des Nucleus olivaris, deren Signale über ein Divergenzgitter auf n Outputneuronen des Kerns verteilt werden, bezeichnen wir als erzeugende Inputneuronen.
Definition: Divergenzgrad
Der Divergenzgrad ist gleich der Anzahl der Outputneuronen eines Divergenzgitters.
Je zwei Inputneuronen verteilten ihre Erregung auf n Outputneuronen. Diese waren entlang der Verbindungsstrecke zwischen ihnen etwa gleichabständig verteilt. Welche Gründe mag es dafür gegeben haben? Denkbar wäre auch, dass sich die Erregung kreisförmig um die beiden Inputneuronen verteilt hätte. Eine kugelförmige Verteilung schied aus, weil der Nucleus olivaris eine Neuronenfläche darstellt, die lediglich sackartig gekrümmt war.
Hier erinnern wir uns an das Richtungstheorem des Neuralrohr-Nervensystems. Jede Axonart wählte - wenigstens in der Frühphase der Evolution - eine von drei Richtungen, die zueinander orthogonal ausgerichtet waren. Daher verliefen die Verbindungsaxone zwischen den Input- und Outputneuronen im Nucleus olivaris alle parallel zueinander. Denkt man sich das Lebewesen wie einen Fisch waagerecht ausgerichtet, so hatte der Nucleus olivaris in etwa die Körperform und verlief auch länglich von vorn nach hinten. Rechtwinklig zu dieser Richtung verliefen die Verbindungsaxone zwischen Input- und Outputneuronen - alle parallel zueinander. Genauer genommen verliefen diese Axone entlang von Kreislinien, die dem Körperumfang entsprachen. Dies ist der Grund dafür, dass der Nucleus olivaris die Parallelschaltung von linearen Divergenzgittern darstellte und keine ebenen Divergenzgitter besaß.
Die zweite Erweiterungsphase des Cerebellums begann allmählich und parallel zur ersten und dritten. Es spricht einiges dafür, dass sie nie beendet wurde. Offenbar haben Wirbeltiere mit einer höheren Entwicklungsstufe diese Phase mit höherer Intensität durchlaufen. Der Beginn dieser Phase hatte einen einfachen Grund: Rezeptoren und Neuronen hatten keine unbegrenzte Lebensdauer. Wenn wichtige Rezeptoren und Nervenzellen auf Grund einer geringeren Lebensdauer, einer Verletzung oder Krankheit abstarben, wurde die Funktionsfähigkeit des gesamten Organismus beeinträchtigt, was sich auf die Überlebensfähigkeit auswirkte. Eine redundante Signalübertragung konnte sicherstellen, dass Signale auch dann ihr Ziel erreichten, wenn einzelne Nervenzellen und deren Axone und Dendriten abstarben.
Eine frühe Form der redundanten Signalübertragung entwickelte sich im Rückenmark. Signale wurden auf mehreren Axonen übertragen. Fiel ein Axon aus, so übertrugen die verbleibenden die Signale. Es gibt im Rückenmark deutlich mehr Axonleitungen als etwa zuführende Ganglienzellen der Spinalganglien. Doch der verfügbare Raum im Rückenmarkskanal war begrenzt. Viel mehr Platz gab es auf der Höhe der Eingangsetage des Urhirns, dort konnte sich das Neuralrohr bereits aufblähen, wodurch mehr Raum zur Verfügung stand. Die Signaldivergenz entwickelte sich zunächst im Nucleus olivaris.
Durch die starke Zunahme der Projektionsneuronen des Nucleus olivaris erfolgte eine starke Aufblähung dieser Struktur, die bei gleicher Länge zunehmend sackartig wurde und Falten bildete, um die immer größer werdende Oberfläche dieses Gebildes im verfügbaren Raum unterzubringen. Dies sieht man heute noch auf Schnittbildern auf der Höhe dieses Kerns. In der nachfolgenden Abbildung, die Professor Leo Gerbilsky aus Kiel zur Verfügung stellte, sieht man die beschriebene Struktur in grüner Farbe dargestellt.
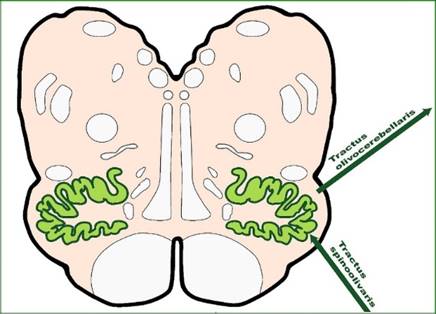
Abbildung 24 - Der Nucleus olivaris und seine Struktur
Stellt man sich den Körper des Lebewesens wurmförmig vor, so bilden die zwei Olivenkerne zusammengenommen im Prinzip ebenfalls eine wurmförmige Struktur, die jedoch durch die starke Signaldivergenz aufgebläht wurde und daher zwar die gleiche Länge vom Kopf bis zum Schwanz hat, jedoch einen deutlich größeren Durchmesser aufweist. Die Aufblähung erfolgt demnach nur in einer Dimension. Der Platzbedarf führte zur Faltung der Oberfläche.
Das Objekt, welches hier als Nucleus olivaris bezeichnet wird, war (vereinfacht) eine Fläche, die in etwa die Form eines Zeppelins hatte. Sie besaß daher als Fläche nur zwei Dimensionen. Jede Hälfte diente einer Körperseite.
Die Neuronen des Nucleus olivaris projizierten in einer Punkt-zu-Punkt-Abbildung als Kletterfasern in die Purkinjezellen, beide Neuronenarten waren (damals) zahlenmäßig gleichstark. Daher kam es zu einer ebenso starken Aufblähung der Cerebellumrinde, in der die riesige Menge von Purkinjezellen untergebracht werden musste. Auch hier erfolgte - analog zu den Veränderungen im Nucleus olivaris - eine Faltenbildung, um den begrenzt verfügbaren Raum möglichst optimal auszunutzen.
Theorem der enormen Zunahme der Purkinjezellen im Spinocerebellum
Die Signaldivergenz im Nucleus olivaris hatte eine enorme Zunahme der Anzahl der Purkinjezellen zur Folge, die Anzahl der Outputneuronen der Kleinhirnkerne stieg ebenso an.
Da auf dieser Evolutionsstufe jedes Outputneuron des Nucleus olivaris in genau eine Purkinjezelle projizierte, bildete die Cerebellumrinde ein Neuronenmodell des Nucleus olivaris. Sie dehnte sich ebenso aus und bildete eine faltige Struktur. Die beiden Kleinhirnhälften bilden zusammen ein Körpermodell des Tieres. Beim einfachen, wurmartigen Wesen wäre dies eine Art Schlauch, der in etwa die Körperform hätte, jedoch wegen der starken Signaldivergenz im Durchmesser deutlich vergrößert war. Die Richtung der Parallelfasern entsprach der Körperachse vom Kopf zum Schwanz, die Ebene der Purkinjezellen war dazu senkrecht orientiert. Die Moosfasern, die sich später bildeten, repräsentierten in diesem Modell die gleiche Richtung wie die Körperachse, obwohl das Cerebellum zum Cortex um etwa 90 Grad gedreht war.
Theorem des Körpermodells des Spinocerebellums
Beide Cerebellumhälften aneinandergefügt bildeten ein Körpermodell, welches bei wurmartigen Tieren ebenfalls wurmartig war. Die Körperachse im Modell verlief parallel zu den Parallelfasern. Durch die starke Signaldivergenz im Nucleus olivaris wurde der Durchmesser dieses Körpermodells stark vergrößert im Vergleich zum Zustand vor der Signaldivergenz. Die Raumforderung führte zur Faltung der Struktur, die Faltenrichtung im Modell verlief parallel zur Körperachse im Modell. Die Bilateralität führte zur Aufspaltung in zwei Cerebellumhälften.
Bei Lebewesen mit Extremitäten kamen seitliche Zylinder hinzu, die die Neuronen der Extremitäten repräsentierten, auch diese wiesen durch die Signaldivergenz ein starkes Wachstum des Durchmessers auf und bewirkten infolge des Raummangels ebenfalls eine Faltenbildung.
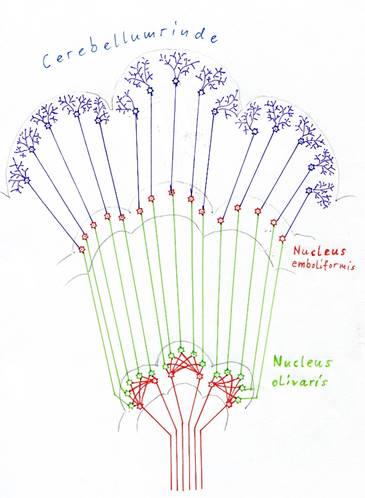
Abbildung 25 - Signaldivergenz im Nucleus olivaris und im Cerebellum
Definition: Elementarzeile
Diejenigen Purkinjezellen, deren Kletterfaserinput über ein Divergenzgitter von zwei erzeugenden Inputneuronen des Nucleus olivaris abgeleitet wird, bezeichnen wir als Elementarzeile von Purkinjezellen. Beim Divergenzgrad n besteht sie aus n Purkinjezellen.
Die Purkinjezellen einer Elementarzeile sind im Cerebellum in der gleichen Ebene angeordnet wie die relativ flachen Dendritenbäume dieser Zellen. Die Purkinjezellen der hintereinander angeordneten Elementarzeilen zu den verschiedenen erzeugenden Inputsignalen des Nucleus olivaris bilden im Cerebellum kleine Windungen, rechtwinklig dazu verlaufen die Parallelfasern.
Auch im Kleinhirnkern des Spinocerebellums gab es nun, nach der Signaldivergenz, eine viel größere Anzahl von Outputaxonen dieses Muskelpaares, die ihrerseits im Nucleus ruber der Gegenseite eintrafen. Die Größenzunahme dieses Outputkerns war ebenso zwangsläufig. Dort wurde die Signaldivergenz rückgängig gemacht. Das Axonbündel projizierte nun wieder auf genau zwei Outputneuronen, die ihrerseits zu einem Paar von Motoneuronen zogen. Diese waren dem ursprünglichen Muskelpaar zugeordnet.
Theorem des Hautpinputs des Spinocerebellums
Der Hauptinput des Spinocerebellums nach der Herausbildung der Signaldivergenz im Nucleus olivaris bestand aus den Kletterfasersignalen, die vom Nucleus olivaris geliefert wurden.
Theorem der Signalkonvergenz im Nucleus ruber
Die im Nucleus olivaris hervorgerufene Signaldivergenz wurde im Nucleus ruber rückgängig gemacht.
Mit der Herausbildung der Signaldivergenz im Nucleus olivaris und der Rückgängigmachung dieser Signaldivergenz im Nucleus ruber bildeten die Outputneuronen im Nucleus ruber immer größere Dendritenbäume, sie entwickelten sich zu magnocellularen Neuronen. Diese bildeten im Verlaufe der Evolution einen eigenen Kernanteil.
Theorem des magnocellularen Kernanteils im Nucleus ruber
Die Rückgängigmachung der Signaldivergenz im Nucleus olivaris erforderte die Bildung magnocellularer Neuronen im Nucleus ruber, die dort einen eigenen Kernanteil bildeten.
Ein Inputneuron des Nucleus ruber empfing nun eine ganze Reihe von Axonen aus dem Kleinhirnkern, die zu einem Muskelpaar gehörten und somit nur zwei Outputneuronen kontaktieren konnten. Dies hatte zur Folge, dass jedes Outputneuron des Nucleus ruber anstelle eines Axons eine größere Axonanzahl empfing. Diese Neuronen brauchten einen viel größeren Dendritenbaum und damit auch einen größeren Zellkörper. Sie wurden magnocellular. Mit dem Übergang zur Signaldivergenz im Nucleus olivaris entstand im Nucleus ruber ein großzelliger (magnocellularer) Kernanteil, der bei heutigen Wirbeltieren ebenfalls vorhanden ist.
In der folgenden Darstellung ist der Weg für zwei komplementäre Signale dargestellt, beispielsweise für die Muskelspannungsrezeptoren der zwei Muskeln eines Beugegelenks. Die Signale fA und fB der zwei zugehörigen Rezeptoren erreichen - vom motorischen Cortex absteigend - den Nucleus ruber, der zum Nucleus olivaris der Gegenseite projiziert. In diesem Kern findet die Signaldivergenz statt. In unserer Darstellung verteilen sich die zwei Inputsignale beispielhaft auf 6 Projektionsneuronen, die zu 6 Purkinjezellen der Rinde des Spinocerebellums projizieren. Diese schalten die Signale auf den hemmenden Transmitter GABA um und projizieren hemmend in 6 Neuronen des Cerebellumkerns.
Diese werden - alle sechs - durch ein Mittelwertsignal aus der Formatio reticularis dauererregt, so dass die Hemmung durch die Purkinjezellen zu einer Signalinversion führt.
Die sechs invertierten Signale erreichen den parvozellularen Teil des Nucleus ruber, wo eine starke laterale Hemmung durch Interneuronen dazu führt, dass nur noch ein Outputaxon aktiv feuert, die übrigen jedoch inaktiv sind. Aber jedes der sechs Outputneuronen projiziert auf genau zwei Outputneuronen im magnozellularen Teil des Nucleus ruber. Hier findet die Umkehrung der Signaldivergenz statt. Der Output des Nucleus ruber (genauer seines magnozellularen Anteils) besteht aus zwei Signalen, die nun zur Ansteuerung der Gegenspielermuskeln genutzt werden. Der Muskel, der mit seinem Muskelspannungsrezeptor das Signal fA erzeugte, erhält vom Nucleus ruber das invertierte Signal fD, der andere das Signal fC. Die mathematischen Zusammenhänge werden in diesem Kapitel nachfolgend hergeleitet.
Wir müssen beachten, dass die räumliche Anordnung der beteiligten Neuronenkerne hier in dieser Darstellung keinerlei Rolle spielt, sondern nur ihre Reihenfolge. Wir wählen in unserer schematischen Darstellung einen symbolischen Signalverlauf von oben nach unten.
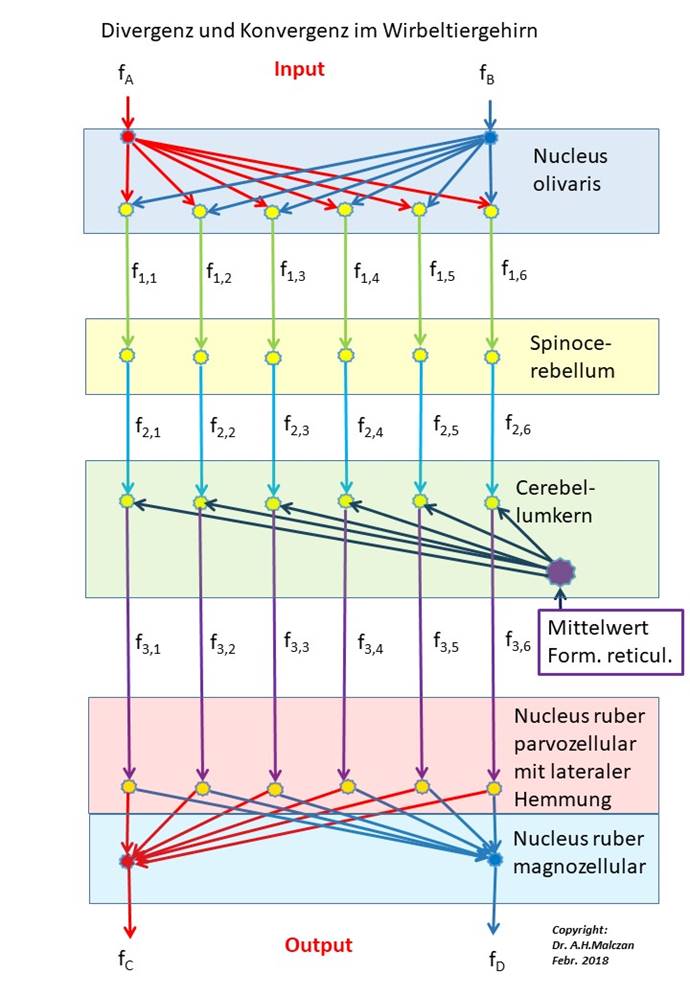
Abbildung 26 - Divergenz und Konvergenz im Wirbeltiergehirn
Die Signaldivergenz des Nucleus olivaris setzt sich im Cerebellum und im Kleinhirnkern fort. Sie wird erst im Nucleus ruber aufgehoben.
Für die später erfolgende mathematische Beschreibung der mit der Divergenz und Konvergenz verbundenen Signalveränderungen sind die Feuerraten der Neuronen neben den zugehörigen Axonen angegeben. Sie sind doppelt indiziert. Der erste Index kennzeichnet die Ebene, der zweite die Nummer des Neurons in der entsprechenden Ebene.
Der Algorithmus der Signalverarbeitung in der folgenden Schaltung kann durch 5 Vektoren beschrieben werden:
1. Inputvektor: i = (fA; fB)
2. Vektor der ersten Ebene: v1 = (f1,1; f1,2; f1,3; f1,4; f1,5; f1,6)
3. Vektor der zweiten Ebene: v2 = (f2,1; f2,2; f2,3; f2,4; f2,5; f2,6)
4. Vektor der dritten Ebene: v3 = (f3,1; f3,2; f3,3; f3,4; f3,5; f3,6)
5. Outputvektor: o = (fC; fD).
Wir leiten nun die mathematischen Algorithmen für diese Vektoren her. Das wichtigste Nebenergebnis der Signaldivergenz war die abstandsabhängige Signaldämpfung.
Theorem der Signaldämpfung im Nucleus olivaris
Der Nucleus olivaris ist ein Kern der grauen Substanz, die Axone der Inputneuronen verlieren in ihm die Myelinhülle. Daher erfolgt die Signalausbreitung in diesem Kern gemäß der Kabelgleichung für marklose Fasern.
Die Kabelgleichung für marklose Axone beschreibt die Abnahme der Erregung entlang eines Axons, wobei E0 die Ausgangserregung am Axonanfang darstellt und E dem Erregungswert entspricht, der im Abstand x vom Axonanfang gemessen wird:
![]() .
(2.2.1)
.
(2.2.1)
Die Größe λ wird als Längskonstante des Neurons bezeichnet.
Die Erregungsfunktion kann grafisch in einem Diagramm dargestellt werden, hier ist die Erregungsabnahme bei zunehmendem Abstand gut zu erkennen.
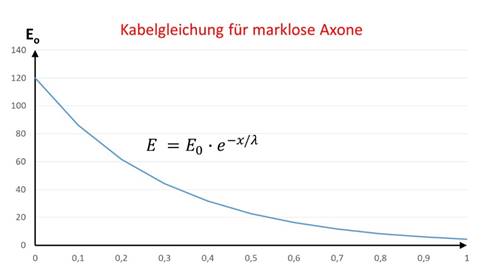
Abbildung 27 - Kabelgleichung für marklose Axone
Vorausgesetzt wird, dass das Axon unmyelinisiert ist und die Erregungsausbreitung unterschwellig erfolgt, also keine Aktionspotentiale auftreten. Diese Form der Erregungsausbreitung beobachtet man bei lokalen, nichtspikenden Interneuronen, die eine Signalübertragung mit graduierten Potentialen realisieren [12]. Die Nichtauslösung von Aktionspotentialen kann erklärt werden durch das Fehlen von spannungsabhängigen Ionenkanälen in der Zellmembran entlang der Axone der Interneuronen.
Wird ein Interneuron über chemische Synapsen durch ein Inputneuron erregt, wodurch seine Membranspannung ansteigt, so wird dieser Spannungsanstieg auf das angeschlossene Outputneuron weitergegeben. Der Anstieg der Membranspannung im Outputneuron wird bewirkt durch einen Ionenaustausch zwischen Interneuron und Outputneuron, der über Transmembranproteine erfolgt, welche die elektrischen Synapsen bilden, die auch als Gap Junction bezeichnet werden. Die als Connexine bezeichneten Moleküle treten bei Wirbeltieren in verschiedensten Zellen auf, so auch im Nervensystem. Sie ermöglichen einen Stoffaustausch zwischen benachbarten Zellen, ohne dem es kein mehrzelliges Leben geben würde. Ekrem Dere beschreibt im Werk -Gap Junctions in the Brain: Physiological and Pathological Roles- [114] das Auftreten von Connexinen im Gehirn von Wirbeltieren.
Connexine werden üblicherweise nach ihren Molekulargewichten benannt, z. B. ist Cx36 das Connexinprotein von 36 kDa. Cx36-positive Neuronen wurden nach [114] nachgewiesen in der Retina, im Gyrus dentatus, in den Regionen CA1, CA3 und CA4 im Hippocampus, im cerebralen und periformen Cortex, in der Amygdala, im Cerebellum, im Mesencephalon, im Nucleus suprachiasmaticus, im Thalamus, Hypothalamus und in verschiedenen Hirnnervenkernen. Gap Junction mit Cx36 wurden ebenso im olivocerebellaren System vorgefunden. In [114] werden viele Klassen von Connexinen hinsichtlich ihres Vorkommens im Gehirn analysiert. Wir können also davon ausgehen, dass speziell im Nucleus olivaris solche aus Connexinen aufgebauten elektrischen Synapsen real existieren.
Eine hinreichende neuronale Erregung solcher Interneuronen kann in nachgeschalteten Neuronen über die örtliche und zeitliche Summation zur Überschreitung der Auslöseschwelle für Aktionspotentiale führen. Beispielsweise werden in der Retina die Aktionspotentiale der Ganglienzellen über graduierte Potentiale der retinalen Interneuronen verursacht. Wir postulieren hier eine analoge Erregungsausbreitung im Olivenkern.
Aus der Kabelgleichung für marklose Fasern kann direkt auf die Feuerrate f geschlossen werden, die ein Neuron hat, welches von einem Inputneuron mit der Feuerrate f0 den Abstand x hat und mit diesem über ein markloses Axon verbunden ist. Hier tritt anstelle der Erregung E die Feuerrate f auf.
Die grafische Darstellung der Feuerratenfunktion in Abhängigkeit vom Abstand x zeigt die nachfolgende Abbildung.
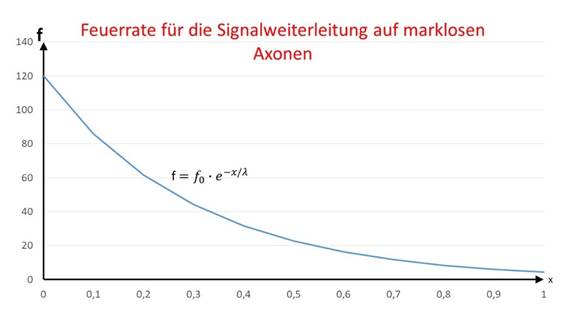
Abbildung 28 - Feuerrate für die Signalweiterleitung auf marklosen Axonen
Nun kann ein Outputneuron durchaus mit zwei Inputneuronen verbunden sein. Und letztlich kann eine Gruppe von Outputneuronen mit zwei gemeinsamen Inputneuronen verbunden sein. Dann können wir von Signaldivergenz sprechen. Die Anzahl der Inputneuronen ist hier immer deutlich kleiner als die Anzahl der Outputneuronen.
Wir analysieren zunächst die Funktionsweise des Divergenzgitters, welches die erste Substruktur aus der Abbildung 28 darstellt.
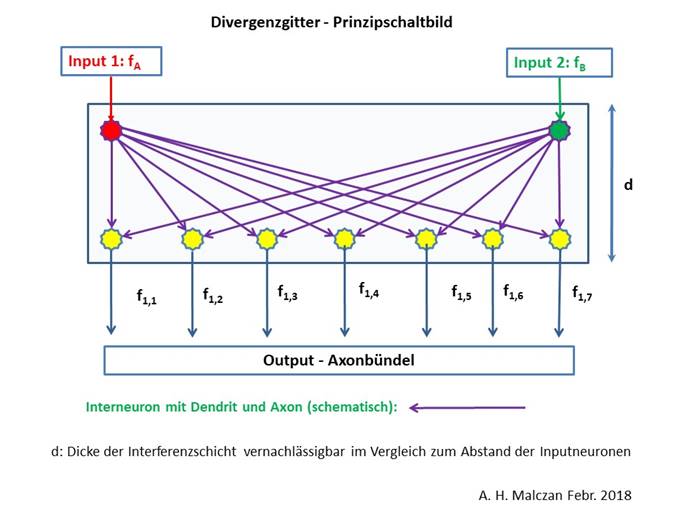
Abbildung 29 - Divergenzgitter im Nucleus olivaris - Prinzipschaltbild
Die Inputfeuerraten können wir zu einem Inputvektor zusammenfassen:
i = (fA; fB) (2.2.3)
Die Outputfeuerraten können wir ebenso zu einem Outputvektor zusammenfassen, wobei n die Anzahl der Outputneuronen darstellt:
v1 = (f1,1; f1,2; f1,3; f1,4; -, f1,n) (2.2.4)
Wir können nun mittels der Kabelgleichung die Erregung der einzelnen Outputneuronen ermitteln, wobei die Feuerrate der Inputlieferanten als Faktor in die Erregungsübertragung eingeht. Dadurch bekommen wir Zwischenwerte für die Erregungsfunktion an den Stellen, an denen die Outputneuronen ihre Erregung erhalten.
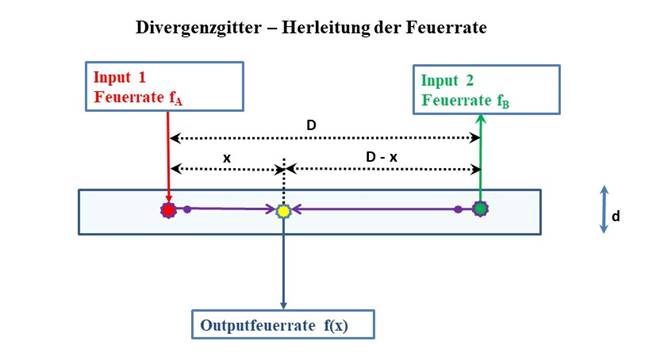
Abbildung 30 - Divergenzgitter - Herleitung der Feuerrate
Die Erregung f(x) der Outputneuronen eines Divergenzgitters kann durch eine
Funktionsgleichung beschrieben werden, die als Parameter die Feuerraten fA
und fB
und die konstanten Größen λ und D enthält und in der die Variable x den Abstand
des Outputneurons von linken Inputneuron angibt. Wir werden diese Funktion f(x)
als Erregungsfunktion des (linearen) Divergenzgitters bezeichnen:
![]() (2.2.5)
(2.2.5)
Die Feuerraten der Outputneuronen sind nicht nur theoretisch berechenbar, sondern auch real vorhanden. Sie könnten beispielsweise durch Messung vor Ort nachgewiesen werden.
Wir können die Gleichung (14.4) mit Fug und Recht als virtuelle Erregungsfunktion eines linearen Divergenzgitters bezeichnen. Denn sie erlaubt die Ermittlung der Feuerrate, die ein Outputneuron hätte, wenn es sich an der Stelle x im Gitter befände.
Die Verwendung der virtuellen Erregungsfunktion erlaubt es, von den real existierenden Dendriten und Axonen der Neuronen zu abstrahieren. Wir betrachten die Erregungsausbreitung in einem kontinuierlichen Ersatzmodell. Dieses ist vergleichbar mit der Schallausbreitung des Schalls mehrerer Schallquellen oder mit der Wärmeausbreitung bei mehreren Wärmequellen. Ebenso vergleichbar ist dieses Modell mit der elektrischen Feldstärke bei mehreren vorhandenen elektrischen Ladungen oder gar mit dem Schwerefeld von Himmelskörpern und den zwischen ihnen wirkenden Kräften. Hier zeigt sich die Schwachstelle der numerischen Simulation von neuronalen Schaltungen durch die Nachbildung ihrer Axone, Dendriten und Synapsen im europäischen Human Brain Projekt. Es gibt Modelle, die ganz ohne Synapsen auskommen und die Signalverarbeitung dennoch erklären können, indem sie sich auf die Signalausbreitung beschränken.
Der Output des Divergenzsystems ergibt sich durch Übernahme der Erregungswerte der virtuellen Erregungsfunktion durch die Abtastneuronen, die wie kleine Messfühler den lokalen Erregungswert übernehmen und feuerratencodiert zu den Signalempfängern weiterleiten.
Die Outputneuronen interpolieren quasi die Erregungsfunktion f(x) an den Zwischenstellen, an denen sie sich befinden. Wir bezeichnen eine solche Schaltung als Divergenzgitter. Sie ist ein Neuronengitter, welches die Erregungsfunktion f(x) interpoliert und die Funktionswerte an den Abtaststellen als Output liefert. Die Outputneuronen bezeichnen wir als Abtastneuronen. Da die Abtastung entlang einer Linie (genauer einer Strecke) erfolgt, handelt es sich um ein lineares Divergenzgitter.
Stellt D den Abstand zwischen
beiden Inputneuronen dar, n ihre Anzahl und ![]()
deren Abstand, so gilt für die Erregung fk des Neurons Nk die Gleichung
![]() (2.2.6)
(2.2.6)
Damit lässt sich die Art der Signalverarbeitung in einem Divergenzgitter auf eine mathematische Transformation â-- zurückführen, die den zwei Inputfeuerraten fA und fB sowie den Zahlen λ n und einen Divergenzvektor aus n Komponenten zuweist.
Theorem der Divergenztransformation
Die Divergenztransformation
![]()
mit
![]()
und
![]()
weist jedem Inputvektor i = (fA; fB) einen eindeutig bestimmten n-stelligen Outputvektor zu. Die neuronale Realisierung erfolgt in einem Divergenzgitter. Die Werte der Vektorkomponenten entsprechen den Abtastwerten einer Erregungsfunktion an den Abtaststellen.
Die Erregungsfunktion f(x) besitzt zwei Maxima, jeweils links an der Stelle x = 0 und rechts bei x = D. Dazwischen besitzt sie ein Minimum. Dieses lässt sich über die erste Ableitung von (2.2.5) berechnen, die man anschließend gleich null setzen muss, um die Bedingung für das Minimum zu erhalten.
![]() .
(2.2.7)
.
(2.2.7)
Als Ergebnis erhält man die Erkenntnis, dass die Erregungsfunktion f(x) ein lokales Minimum an der Stelle
![]() (2.2.8)
(2.2.8)
![]() (2.2.9)
(2.2.9)
besitzt . Je nachdem, in welchem Verhältnis die Inputfeuerraten fA und fB zueinander stehen, wird das Minimum an einer anderen Stelle x* angenommen. Eine Multiplikation beider Feuerraten fA und fB mit einem beliebigen Faktor a > 0 verändert nicht die Lage des Minimums, der Faktor kürzt sich in (14.6) heraus. Daher ist es zweckmäßig, sich auf den Feuerratenquotienten q zu beschränken, der nachfolgend definiert wird:
![]()
Diese Beziehung lässt sich nach dem Parameter q auflösen, dann ergibt sich eine Gleichung, die wir als Codierungsfunktion q(x) bezeichnen werden:
![]() (2.2.10)
(2.2.10)
Mit ihr lässt sich berechnen,
welches Signalstärkeverhältnis q = fA/fB
vorliegen muss, damit in einem Divergenzgitter das Erregungsminimum an der
Stelle
![]() angenommen wird. Das Signalstärkeverhältnis codiert also die Stelle
angenommen wird. Das Signalstärkeverhältnis codiert also die Stelle
![]() ,
an der das Minimum liegt. Der Outputvektor eines solchen Divergenzgitters ist
ebenfalls minimumcodiert, da er die Feuerratenwerte an den Abtaststellen
enthält, in denen sich die Outputneuronen befinden.
,
an der das Minimum liegt. Der Outputvektor eines solchen Divergenzgitters ist
ebenfalls minimumcodiert, da er die Feuerratenwerte an den Abtaststellen
enthält, in denen sich die Outputneuronen befinden.
Wegen der großen Bedeutung des Feuerratenquotienten fassen wir die Resultate in einem eigenen Theorem zusammen.
Theorem des Zusammenhanges zwischen dem Feuerratenquotienten und dem Abstand der Inputneuronen im Divergenzgitter
Zwischen dem Feuerratenquotienten q, dem Minimalpunkt x* und dem Abstand der Inputneuronen im Divergenzgitter gilt der Zusammenhang
![]() .
(2.2.11)
.
(2.2.11)
Damit gilt auch
![]() (2.2.12)
(2.2.12)
Bekanntlich benötigt ein Divergenzgitter zwei Inputfeuerraten fA und fB. Diese Inputfeuerraten können durchaus von Rezeptoren geliefert werden. Genau diesen Fall untersuchen wir jetzt. Wir brauchen zwei Rezeptoren RA und RB, deren Input ein Divergenzgitter mit n Abtastneuronen speisen möge. Beide Rezeptoren mögen der gleichen Modalität angehören, RA sein vom On-Typ, RB dagegen vom Off-Typ.
Theorem der Signaltransformation von Rezeptorinput durch ein Divergenzgitter
Ein Rezeptor RA messe eine physikalische, chemische oder sonstige Größe, der Messwert h liege im Intervall < hA; hB>, die Feuerrate in der Intervallmitte sei fm, hm sei die halbe Intervallbreite gemäß
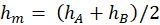 .
(2.2.13)
.
(2.2.13)
und er liefere bei Veränderung der Größe h im Intervall < hA; hB> die On-Feuerrate
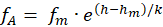 .
(2.2.14)
.
(2.2.14)
Der Rezeptor RB liefere bei Veränderungen der gleichen Größe h die Off-Feuerrate
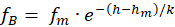 .
(2.2.15)
.
(2.2.15)
Damit sind fA und fB komplementär zueinander, denn es gilt
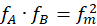 (2.2.16)
(2.2.16)
und
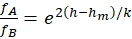 (2.2.17)
(2.2.17)
sowie
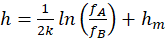 (2.2.18)
(2.2.18)
Die virtuelle Erregungsfunktion des Divergenzgitters mit den Inputwerten fA und fB gemäß
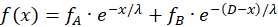 (2.2.19)
(2.2.19)
besitzt ein Erregungsminimum an der Stelle x* gemäß
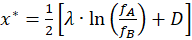 (2.2.20)
(2.2.20)
Einsetzen von (2.2.17) in (2.2.20) liefert als Bedingung für das Vorliegen eines Erregungsminimums die Gleichung
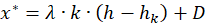 (2.2.21)
(2.2.21)
sowie
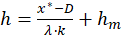 (2.2.22)
(2.2.22)
Aus dem Minimumwert x* lässt sich also eineindeutig der Wert der Urgröße h ermitteln.
Die Divergenztransformation bildet nicht nur das Urintervall auf das Intervall der Feuerraten der Erregungsfunktion ab, sondern das Minimum der Erregungsfunktion codiert den Signalwert der Urgröße. Damit dient das Divergenzgitter der Extremwertcodierung einer Urgröße.
Der Input eines Divergenzgitters besteht aus zwei Signalen, die zueinander invertiert sind. Zwei Rezeptoren bzw. ihre zugehörigen Ganglienzellen, die zueinander invertierte Signale liefern, bezeichnen wir als komplementäre Rezeptoren bzw. Ganglienzellen. Das Signal des einen Rezeptors kann für jeden Wert der detektierte Urgröße in das Signal des zweiten Rezeptors invertiert werden. Als Oberbegriff für den Rezeptor verwenden wir auch den Begriff Detektor.
Theorem der Minimumcodierung in linearen Divergenzgittern
In einem linearen Divergenzgitter wird das Signalstärkeverhältnis der zwei Inputsignale in einen minimumcodierten Signalvektor transformiert. Der Wert der Urgröße, welche über zwei komplementäre Rezeptoren den Input liefert, wird in den Outputsignalen minimumcodiert verschlüsselt.
Lineare Divergenzgitter stellen mathematisch den eindimensionalen Fall dar. Die Erregung breitet sich hier (idealisiert) entlang einer Strecke aus, die die beiden Inputneuronen verbindet. Im zweidimensionalen Fall würde die Erregungsausbreitung in der Ebene erfolgen, wobei hier wenigstens drei, aber auch vier, teils sogar sechs Inputneuronen mitwirken. Ebenso könnte auch eine räumliche Ausbreitung der Inputerregung erfolgen, wobei dann die Inputneuronen in einem zugehörigen Raumgebiet verteilt wären. In der folgenden Abbildung wird ein lineares Divergenzgitter einem ebenen Divergenzgitter gegenübergestellt, wobei Letzteres vier Inputneuronen besitzt.
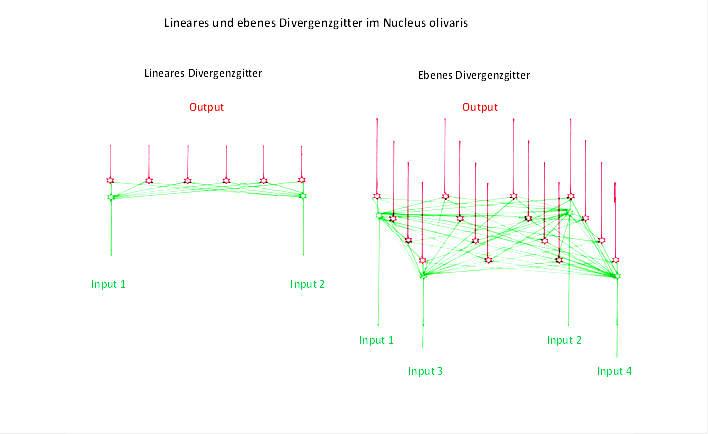
Abbildung 31- Lineares und ebenes Divergenzgitter im Nucleus olivaris
Ein minimumcodierter Signalvektor ist allerdings oft ungeeignet, weil das codierende Neuron minimal erregt ist. Für die motorische Ansteuerung eines Muskels ist solches ein Signal unbrauchbar. Daher ist eine Umwandlung in eine maximumcodierte Darstellung zweckmäßig und wird in der neuronalen Realität auch vorgenommen.
Theorem der Signalinversion von minimumcodierten Signalvektoren
Jeder minimumcodierte Outputvektor des Divergenzgitters im Nucleus olivaris wird durch Signalinversion im Spinocerebellum in einen maximumcodierten Signalvektor des Nucleus interpositus transformiert. Eine laterale Hemmung zwischen den Outputneuronen dieses Kerns überführt den minimumcodierten Outputvektor näherungsweise in einen Outputvektor mit spärlicher Codierung.
Die Signalinversion im Spinocerebellum wurde bereits ausführlich dargestellt. Der Output des Nucleus olivaris trifft über die Kletterfaseraxone bei den Purkinjezellen des Spinocerebellums ein und führt zu deren Erregung. Jede Purkinjezellen übernimmt die Feuerrate des zugehörigen Neurons im Nucleus olivaris. Mit dieser Feuerrate hemmt sie das zugehörige Outputneuron im Cerebellumkern, welches jedoch dauererregt ist. Dadurch wird das Signal invertiert. Das Spinocerebellum bleibt sich in seiner Funktionsweise treu: Jeder Input aus der Olive wird invertiert und stellt den erregenden Output des Spinocerebellums dar.
Bezeichnen wir mit fD die Feuerrate der tonischen Dauererregung im Cerebellumkern und den Outputvektor des Divergenzgitters im Nucleus olivaris mit
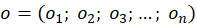 ,
(2.2.23)
,
(2.2.23)
so gilt für den invertierten Outputvektor k aus dem Kleinhirnkern die Beziehung
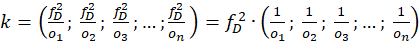 (2.2.24)
(2.2.24)
Hierbei wird ein Signalminimum im Vektor o in ein Signalmaximum im Vektor k überführt.
Bei einer Signalinversion kehrt sich der Monotonieverlauf um, aus einem Minimum wird. Das maximal erregte Outputneuron kann nun über das angeschlossene Motoneuron eine motorische Reaktion hervorrufen, die bei der Minimumcodierung ausgeschlossen war.
Beispielhaft dargestellt im nachfolgenden Diagramm ist die Überlagerung zweier Erregungsfunktionen in einem Divergenzgitter. Die blaue Funktion stellt die Feuerrate des linken Inputneurons dar, dessen Erregung entlang eines Axons nach rechts weitergegeben wird, wobei eine exponentielle Dämpfung entsprechend der Kabelgleichung für marklose Fasern auftritt. In der Farbe braun dargestellt ist die Feuerrate des rechten Inputneurons, dessen Erregung sich nach links entlang des Axons ausbreitet und ebenfalls abstandsabhängig gedämpft wird.
Die gelb dargestellte Funktion entsteht durch reine Addition dieser beiden Inputerregungen und ist eine minimumcodierte Funktion. Durch Signalinversion - also die Hemmung eines Dauersignals, welches selbst eine konstante Feuerrate besitzt, entsteht die grau dargestellte Funktion, die eine maximumcodierte Funktion darstellt.
Die durch Überlagerung entstehende Erregungsfunktion ist grau dargestellt, die durch Inversion gewonnene gelb. Die invertierte Funktion besitzt genau dort ein Maximum, wo die Originalfunktion ein Minimum aufweist.
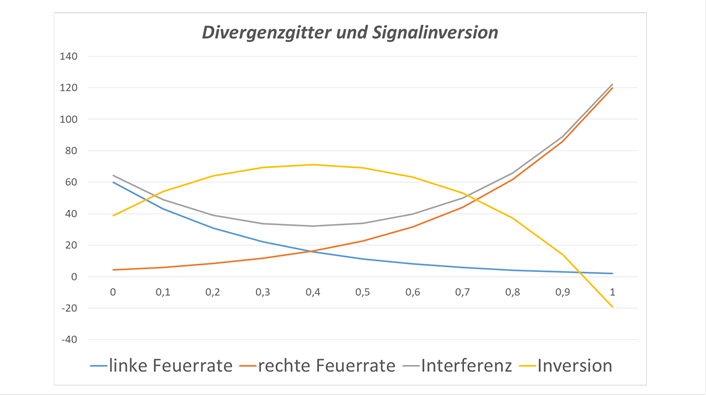
Abbildung 32- Divergenzgitter und Signalinversion
Im obigen Diagramm wird die Interpolation mit stetigen Funktionen dargestellt. In Wirklichkeit erfolgt die Inversion punktweise, jeweils durch die beteiligten Neuronen.
Der invertierte Signalverlauf eines Divergenzgitters kann daher als Balkendiagramm dargestellt werden. Nachfolgend wählen wir als Signalmittelwert den Wert von 250. Er wird vom Output des Divergenzgitters relativ gehemmt, so dass sich folgende Darstellung ergibt:
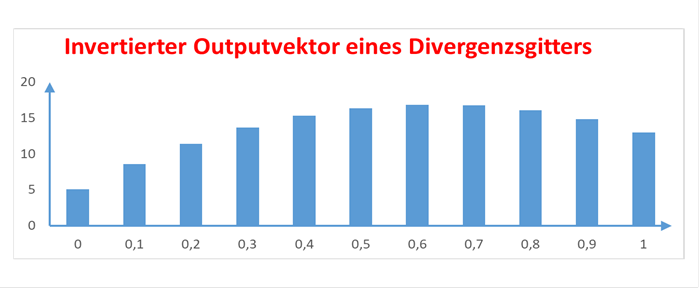
Abbildung 33- Invertierter Output eines Divergenzgitters
Man sieht, dass es neben dem Extremwert auch Nebenwerte gibt, die schwächer sind. Genau diese Werte muss eine nachfolgende neuronale Schaltung eliminieren, so dass nur noch ein Outputneuron maximal erregt ist, die übrigen jedoch völlig inaktiv sind. Dies kann durch die eine starke laterale Nachbarhemmung erreicht werden.
Theorem der Extremwertselektion
Wird ein maximumcodierter Outputvektor auf eine Gruppe von Outputneuronen eines Kerns übertragen, in dem es eine starke laterale Hemmung gibt, so wird dieser Outputvektor in einen digitalen Vektor überführt, der nur noch an einer Position eine maximale Feuerrate aufweist, während an den übrigen Positionen die Feuerrate gleich null ist.
Wir nennen einen solchen Vektor einen Elementarvektor. Nur an genau einer Vektorposition ist die Feuerrate größer Null, auf den übrigen Positionen sind die Werte gleich null.
Beispielsweise bleibt im Diagramm von Abbildung 20 nach einer Extremwertselektion durch starke laterale Hemmung nur noch ein Outputneuron aktiv, wie nachfolgendes Diagramm verdeutlicht.
Abbildung 34- Output Divergenzgitter nach Extremwertselektion
Zu Recht kann man diese Transformation als Digitalisierung bezeichnen.
Der minimumcodierte Vektor aus (2.2.23) könnte beispielsweise folgendes Aussehen:
o = (257,0; 254,2; 252,0; 250,5; 249,5; 249,2; 249,5; 250,5; 252,0; 254,2; 257,0) (2.2.25)
Invertiert man ihn an einem Dauersignal mit der Feuerrate von fD = 280, so erhält man den maximumcodierten Vektor
o* = (305; 308,4; 311,1; 313,6; 314,2; 314,6; 314,2; 312,9; 311,1; 308,4; 305) (2.2.26)
Dieser Vektor hat ein Maximum an der sechsten Komponente, es hat den Wert 314,6.
Eine Extremwertselektion würde dafür sorgen, dass alle übrigen Komponenten, deren Wert kleiner als das Maximum ist, total unterdrückt würden und den Wert 0 erhielten. Damit wäre der Ergebnisvektor o** nach der Extremwertselektion der folgende:
o** = (0; 0; 0; 0; 0; 314,6; 0; 0; 0; 0; 0) (2.2.27)
Von allen elf Outputneuronen, die mit ihren Feuerraten diesen Vektor repräsentieren, hätte nur das sechste in der Reihe eine Feuerrate von 314,6, während alle übrigen Neuronen von ihm total gehemmt würden und die Feuerrate Null hätten. Und seine Feuerrate läge deutlich über der mittleren Feuerrate des Mittelwertsignals, da das Quadrat der mittleren Feuerrate durch die Feuerrate des Minimums aus dem minimumcodierten Vektor zu dividieren ist, um die maximale Feuerrate des nunmehr invertierten Signals zu erhalten. Eine solche Codierungsform wird als spärliche Codierung bezeichnet.
Theorem der spärlichen Codierung
Die Extremwertselektion überführt einen minimumcodierten Signalvektor in einen Signalvektor mit spärlicher Codierung.
Die Extremwertselektion erfordert eine besondere Art der lateralen Hemmung, die nur mit schnellleitenden Axonen zu erreichen ist, die entweder dicker sind oder eine Myelinhülle besitzen. Das Neuron, welches die stärkste Zunahme der Membranspannung aufweist, feuert als erstes sein Aktionspotential ab. Dieses erregt fast unverzögert die angeschlossenen hemmenden Interneuronen, die ihrerseits sofort die Nachbarneuronen hemmen, auch die, die weiter entfernt sind. Dazu müssen diese hemmenden Interneuronen schnellleitende oder myelinisierte Axone besitzen. Sie bilden unterhalb der Projektionsneuronen eine Hemmungschicht, in der die waagerecht verlaufenden Axone ein weißes Geflecht bilden, falls sie myelinisiert sind. Die weiße Farbe wird durch die Myelinscheiden der Axone verursacht.
Sobald das Neuron an der Stelle der maximalen Erregung sein Aktionspotential abfeuert, wird über die angeschlossenen Hemmungsneuronen die zwischenzeitlich aufgebaute Erregung der übrigen Neuronen völlig vernichtet, weil bei gehemmten Neuronen quasi eine Art elektronischer Kurzschluss verursacht wird.
Theorem der Substrukturen mit Extremwertselektion
Eine Extremwertselektion findet im Nucleus ruber statt sowie in den Thalamuskernen und in den Outputkernen des Spinocerebellums. Weiterhin kann eine Extremwertselektion in den Outputkernen der Amygdala stattfinden.
Theorem der Digitalisierung einer Urgröße durch ein Divergenzgitter
Detektieren zwei komplementäre Rezeptoren den Wert einer Urgröße u im Intervall <uA ; uB>, welches in n gleichgroße Teilintervalle T1, T2, T3, -, Tn unterteilt ist, so transformiert ein Divergenzgitter aus n gleichabständigen Outputneuronen O1, O2, O3, - , On dieses Inputtupel in einen Outputvektor aus n Komponenten derart, dass das k-te Outputneuron Ok genau dann und nur dann minimal erregt ist, wenn der Wert der Urgröße u im k-ten Teilintervall Tk liegt. Dies entspricht einer Digitalisierung.
In einem nachgeschalteten Inversionsgitter aus n Neuronen hat das k-te Neuron dann und nur dann eine maximale Erregung, wenn der Wert der Urgröße u im k-ten Teilintervall Tk liegt. Ist ein aus n Neuronen bestehendes Gitter mit Extremwertselektion nachgeschaltet, so ist das k-te Neuron dann und nur dann maximal erregt, wenn der Wert der Urgröße u im k-ten Teilintervall Tk liegt, während die übrigen Neuronen unerregt sind.
Eine neuronale Digitalisierungsschaltun, bestehend aus der Hintereinanderschaltung eines Divergenzgitters, eines Inversionsgitters und eines Gitters mit Extremwertselektion leistet in etwa das gleiche wie ein digitales Fieberthermometer, bei dem die gemessene Temperatur nicht als Zahl, sondern auf einem beschrifteten Zahlenstrahl (ähnlich einem Metermaßstab) abgebildet wird dadurch, dass in eine Reihe von Leuchtdioden nur genau diejenige aufleuchtet, unter der die zutreffende Zahl dargestellt ist. Dies entspricht auch dem Zahlenformat. Neuronale digitalisierte Werte kennen keine Ziffern, sondern werden auf einem Zahlenstrahl dargestellt, der passend zur gemessenen Urgröße beschriftet ist und nur eine endliche Menge von Zahlenwerten aufweist.
Die Signaldivergenz im Nucleus olivaris führte zur Vervielfachung der Neuronenanzahl. Anstelle von je zwei Signalen der Muskelspindeln eines Gelenks gab es nun eine Vielzahl von ihnen. Die motorische Ansteuerung der zwei Muskeln benötigte jedoch nur zwei Signale. Daher mussten diese vervielfältigten Signale durch Signalkonvergenz wieder zusammengeführt werden. Dies wurde im Theorem der Signalkonvergenz im Nucleus ruber bereits dargestellt.
Die Signalkonvergenz können wir ebenfalls mathematisch analysieren. Hier konvergiert der Output einer Neuronenreihe auf zwei Outputneuronen. Wir beschränken uns auf den Teil der Abbildung 28, die das Konvergenzgitter enthält.
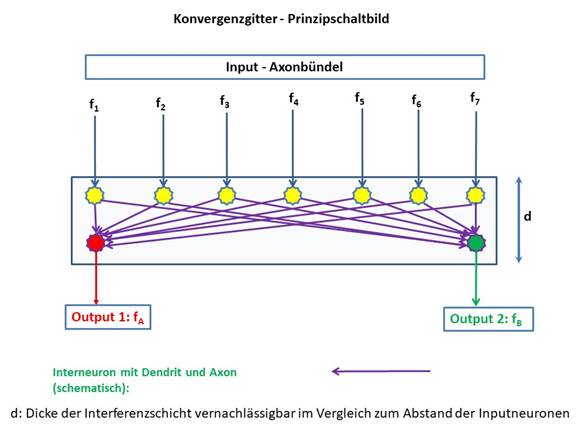
Abbildung 35- Konvergenzgitter - Prinzipschaltbild
Wir erinnern uns, dass der Output eines Divergenzgitters, wenn er eine Signalinversion mit nachgeschalteter Extremwertselektion erleidet, die Besonderheit aufweist, dass (im Normalfall) nur ein Neuron aktiv feuert, während die übrigen total gehemmt sind. Die Lage des Neurons hängt lediglich vom Signalstärkeverhältnis des Inputs des Divergenzgitters ab. Wir können also davon ausgehen, dass nur ein Neuron eine Feuerrate fk ungleich null besitzt. Wir analysieren die mathematischen Hintergründe.
Hierzu betrachten wir zunächst die Erregungsausbreitung von einem einzelnen Inputneuron auf zwei angeschlossene Outputneuronen.
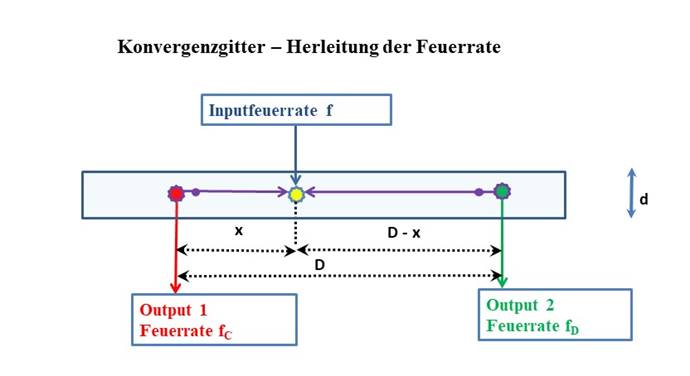
Abbildung 36- Konvergenzgitter - Herleitung der Feuerrate
Hier verteilt sich die Inputerregung, die durch das Inputneuron mit der Feuerrate f geliefert wird, auf die beiden Outputneuronen wieder gemäß der Kabelgleichung für marklose Axone.
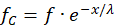 (16.1
(16.1
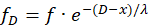 (16.11)
(16.11)
Damit gilt auch
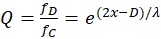 (16.12)
(16.12)
Wir erinnern uns, dass x hier den Wert des Minimums im Divergenzgitter bzw. des Maximums im Inversionsgitter darstellt.
Hierbei stellt der Feuerratenquotient Q den Kehrwert des Wertes q aus dem Divergenzgitter gemäß (14.7) dar. Der Output des Konvergenzgitters ist also bezüglich des ursprünglichen Inputs des Divergenzgitters vertauscht, sein Signalstärkeverhältnis ist der Kehrwert des ursprünglichen Verhältnisses.
Theorem der Hintereinanderschaltung von Divergenzgitter, Inversionsgitter, Extremwertselektion und Konvergenzgitter
Die Hintereinanderschaltung eines Divergenzgitters mit einem Inversionsgitter, einer Extremwertselektion und einem Konvergenzgitter, bei dem der Input aus zwei Signalen mit der Feuerrate fA und fB besteht und das Signalstärkeverhältnis q besitzt gemäß
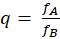 ,
,
liefert als Output zwei Outputsignale mit den Feuerraten fC und fD mit dem Signalstärkeverhältnis
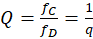 .
.
Befindet sich das signalstärkere Inputneuron des Divergenzgitters rechts (links), so befindet sich der signalstärkere Output des Konvergenzgitters links (rechts), also seitenvertauscht.
Die Vertauschung muss durch eine Spiegelung wieder rückgängig gemacht werden,
Die Signaldivergenz im Nucleus olivaris, gefolgt von einer Signalinversion im Spinocerebellum, einer Extremwertselektion im Nucleus ruber, einer Signalkonvergenz im Nucleus ruber und einer anschließenden Signalspiegelung liefert also den gleichen Output, wie es ihn ohne diese Transformationen gegeben hätte.
Theorem der Unschädlichkeit der Signaldivergenz und -konvergenz
In Bezug auf den motorischen Output hatte die Herausbildung der Signaldivergenz im Nucleus olivaris und die Signalkonvergenz im Nucleus ruber keinerlei Auswirkungen auf den resultierenden Output des Nucleus ruber, wenn zuvor eine Signalspiegelung stattfand.
Die Signalspiegelung fand im Cortex statt. Der Output des Cerebellums wurde aufsteigend an die Neuronen der Klasse 4 auf der sensorischen Seite des Frontalcortex übergeben. Diese übergaben die Signale an Projektionsneuronen der Klasse 3, deren Axone zum motorischen Teil des Frontalcortex zogen. Dort erreichten die Signale die abwärts projizierenden Neuronen der Klasse 5, deren Zielneuronen die Motoneuronen waren.
Die Cortexfläche des Frontalcortex wirkte auf diese Signale in etwa wie ein Hohlspiegel, dadurch wurden die Signale gespiegelt. Diese Signalspiegelung machte die Seitenvertauschung im Divergenzgitter wieder rückgängig. Dies wird im Kapitel über die Entstehung des Frontalcortex genauer beschrieben.
Wenn der motorische Output also nicht wesentlich verändert wurde, stellt sich die Frage nach dem zusätzlichen Nutzen dieser Signaltransformationen. Ein Nutzen lag in der Redundanz, die Schaltung war stabiler, wenn einzelne Neuronen ausfielen.
Ein wesentlich größerer Nutzen bestand darin, dass alle Körperabbilder, deren Signale im Spinocerebellum einer Signaldivergenz unterzogen wurden, quasi digitalisiert waren. Der Gelenkwinkel, der sich aus dem Erregungsverhältnis der Muskelspannungssensoren von zwei gegeneinander arbeitenden Muskeln ergab, wurde im Output des Cerebellums in einen maximumcodierten Signalvektor übertragen, der durch die laterale Hemmung zudem spärlich codiert war. Analoges galt für alle anderen sensorischen Größen. Mit zunehmendem Divergenzgrad wuchs die Auflösung dieser Transformation, Gelenkwinkel und andere Größen könnten viel feiner erkannt werden.
Wäre die Herausbildung dieser Algorithmen schädlich gewesen, hätte die Evolution diese Fehlentwicklung beendet. Da sie aber outputneutral war und damit unschädlich, konnte sie sich manifestieren. Es bleibt nur noch zu zeigen, dass diese Entwicklung sogar - im Verlaufe der weiteren Evolution - weitere erhebliche Vorteile mit sich brachte. Diese neuen Vorteile ergaben sich aus der Entwicklung des Pontocerebellums, die in einem selbständigen Kapitel dieser Monografie beschrieben wird. Zuvor analysieren wir die räumlichen Veränderungen im Gehirnsystem, die als Folge der Divergenzentwicklung auftraten.
Erwähnt werden sollte hier, dass die beschriebene Signaldivergenz im Nucleus olivaris nicht nur Auswirkungen auf das Spinocerebellum hatte, sondern auch das Pontocerebellum betraf. Wir erinnern uns: Die Signalklasse der Mittelwertsignale der Neuronenklasse 6 nahm ebenso den Weg über den Nucleus ruber zum Nucleus olivaris und erreichte eine Cerebellumstruktur, die wir als Pontocerebellum bezeichnet haben. Der zugehörige Kleinhirnkern war der Nucleus dentatus. Auch in diesem Abschnitt der Olive erfolgte eine zunehmende Signaldivergenz. Deren Folgen werden im Kapitel 7 beschrieben, welches der Funktionsweise des Pontocerebellums gewidmet ist.
Zusammenfassung zum Spinocerebellum
Mit der Herausbildung der Signaldivergenz im Nucleus olivaris entwickelte sich das Spinocerebellum zu einer Divergenzschaltung, die die paarweise eintreffenden Signale eines zusammengehörenden Muskelpaares in einen maximumcodierten Signalvektor überführte, bei dem das Signalmaximum den Gelenkwinkel verschlüsselte. Eine laterale Hemmung zwischen den zugehörigen Outputneuronen bewirkte beim Outputvektor eine spärliche Codierung. Damit war der Gelenkwinkel prinzipiell digitalisiert. Mit zunehmendem Divergenzgrad stieg die Genauigkeit dieser Winkeldarstellung an und erlaubte dem Lebewesen eine viel feiner steuerbare Motorik.
Auch andere sensorische Größen, die durch komplementäre Signale dargestellt wurden, konnten auf diese Weise digitalisiert werden.
Die Einbeziehung der Mittelwertsignale in dieses System schuf die Voraussetzungen für die spätere Entwicklung des Pontocerebellums.
Das Spinocerebellum nach der zweiten Erweiterungsphase bezeichnen wir hier als das späte Spinocerebellum.
Sowohl das späte Spinocerebellum als auch der zugehörige Nucleus olivaris und der Cerebellumkern bilden ein Körpermodell des Lebewesens. Denkt man sich den Körper der frühen Chordaten etwa länglich und wurmartig, so hatte das Spinocerebellum in etwa die Form eines Zeppelins, durch die Signaldivergenz im Nucleus olivaris wies das Körpermodell des Cerebellums einen deutlich größeren Durchmesser auf als vor der Signaldivergenz. Denkt man sich die Oberfläche des Körpers in schmale Streifen eingeteilt, so sind diese Streifen im Cerebellummodell deutlich verbreitert und bilden jeweils nach außen gekrümmte Bögen. Jeder Streifen repräsentiert eine Gelenkreihe, die von Kopf zum Schwanz verläuft und in der in jedem Segment zwei gegeneinander arbeitende Muskeln die Purkinjezellen eines solchen Bogens mit ihren Signalen versorgen. Das Erregungsminimum in jeder Purkinjereihe eines Bogens codiert den Gelenkwinkel.
Unterhalb der Purkinjezellen verliefen die Moosfasern in einer Richtung, die parallel zur Körperachse verlief. Die Körnerzellen waren topologisch so angeordnet wie die signalliefernden Rezeptoren auf bzw. im Körper verteilt waren. Die Signaldivergenz im Körnerzellsystem wurde realisiert, indem die Axone der Körnerzellen radial in alle Richtungen der Purkinjezellen strebten, die zu einer Reihe in einem Bogen gehörten.
Theorem des Körpermodells des späten Spinocerebellums
Nach der zweiten Erweiterungsphase bildet das Spinocerebellum ein zweischichtiges Körpermodell des Lebewesens, bestehend aus zwei bilateralen Hälften.
Das Körpermodell war ein Streifencortex mit radialer Expansion und Bogenbildung. Jedem Gelenk war ein Bogen zugeordnet. Wegen des annähernd gleichen Aufbaus der Körpersegmente bildeten die Gelenke Gelenkreihen, die vom Kopfsegment zum Schwanzsegment verliefen. Jeder Gelenkreihe war ein Cerebellumbogen aus Purkinjereihen zugeordnet, die vom Nucleus olivaris die durch Signaldivergenz erzeugten Rezeptorsignale der zugehörigen Muskelpaare empfingen.
Die Körnerzellen repräsentierten die Rezeptoren der Muskeln sowie die Tast- und Schmerzrezeptoren, wobei jede Modalität eine eigene Körnerzellschicht bildet, bei der die Topologie der Rezeptoren des Körpers erhalten blieb.
Die Purkinjezellen bilden bogenförmig angeordnete Reihen, die zu jeweils einer Cerebellumwindung gehören. Das Erregungsminimum der Purkinjezellen einer Bogenreihe verschlüsselte den Gelenkwinkel des Gelenks im zugehörigen Segment.
- ← 4.1 Das Rechnen mit neuronalen Signalen
- 4.3 Die zweite Erweiterungsphase des urtümlichen Pontocerebellums →
Monografie von Dr. rer. nat. Andreas Heinrich Malczan